金融工程期末预习

金融工程概述

金融衍生产品

定义

衍生产品是指依赖于其标的资产的金融工具

按形式分类

• 远期（Forward）
• 期货（Futures）
• 互换（Swap）
• 期权（Option）

远期/期货

双方约定在未来的某一个确定时间，按确定的价格买卖一定数量的某种标的金融资产的合约

• 功能：锁定未来的价格
• 与即期（spot ）相区别
• 远期：OTC产品
• 期货：交易所产品

互换

当事人按照商定条件，在约定的时间内，交换一系列现金流的合约

• 利益互换：约定交换的现金流是以一定本金计算的利息现金流的合约

  • 一方支付以固定利率计算的利息现金流
  • 一方支付以合约规定的浮动利率计算的利息现金流

• 货币互换

期权

赋予其购买者在规定的期限内按双方约定的执行价格购买或出售一定数量某种标的资产的权力的合约

买入为看涨期权，卖出为看跌期权

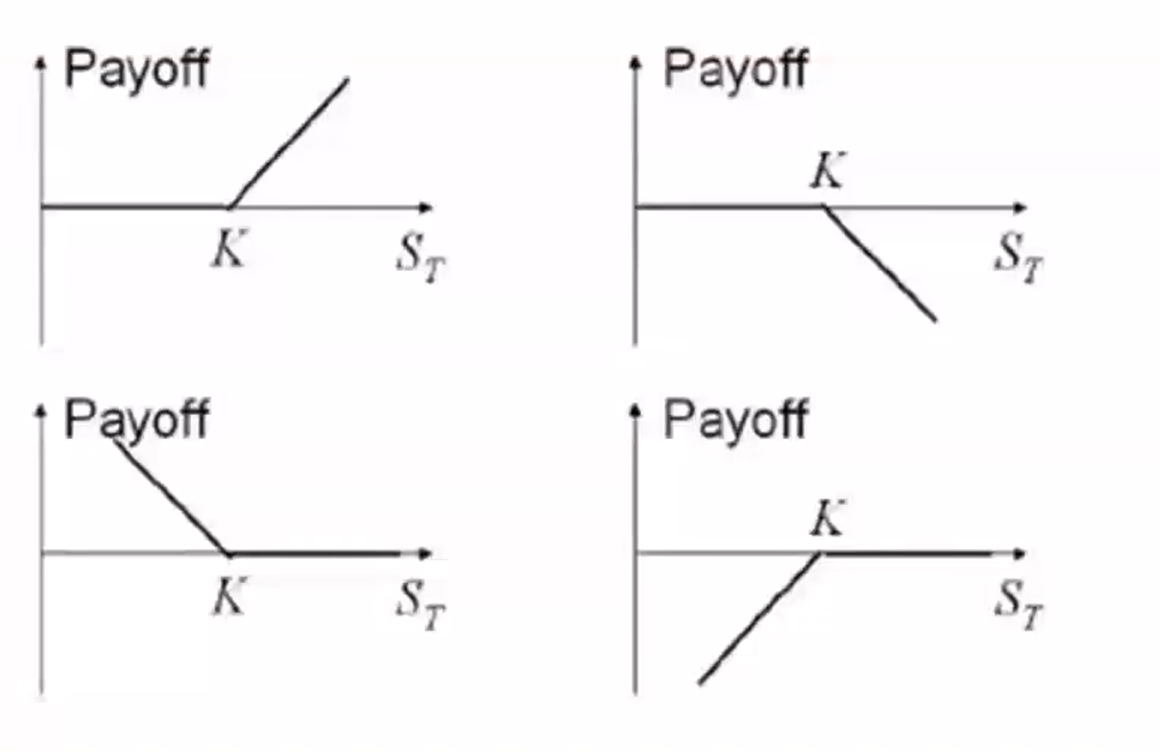
期权的回报（payoff） : 非线性

金融衍生产品：按标的物分类

股票, 债券， 指数， 利率， 汇率， 商品价格， 波动率， 通胀率， 气温， 总统当选

衍生产品的运用

• 投机 （根据不同时间的价格不一致）
• 套期保值
• 套利（根据同一时间的价格不一致）
• 这三种力量在衍生品市场价格决定中的作用：

金融工程的主要分析方法

衍生证券定价的基本假设

• 市场不存在摩擦
• 市场是完全竞争的
• 市场参与者厌恶风险，希望财富越多越好
• 市场不存在无风险套利机会
• 市场不存在对手风险

卖空与套利

• 卖空：在期初资产价格高的时候，借入资产并卖出，在期末资产价格下跌的时候，卖出资产并偿还资产

• 套利：相同的资产应该有同样的价格，否则就存在套利机会。套利活动使得相同资产的价格趋于一致

绝对定价法和相对定价法

• 绝对定价法：运用恰当的贴现率将未来现金流贴现加总（股票和债券）
• 相对定价法：利用标的价格资产与衍生证券价格之间的内在关系，直接根据标的资产价格求出衍生证券价格
• 绝对定价法具有一般性，易于理解，但难以应用；相对定价法则易于实现，贴近市场，一般仅适用于衍生证券

连续复利

各种公式，查书和ppt

远期

金融远期合约定义

双方约定在未来某一确定时间，按确定的价格买卖一定数量的某种金融资产的合约

远期交易机制：OTC

• 特征：分散交易/非标准化

• 优点：个性化、灵活

• 缺点：

  • 流动性较差
  • 违约风险相对较高
  • 信息劣势，市场效率较低

​

远期合约术语

• 多头（Long position） / 空头 (Short position)
• 标的资产
• 交割资产
  • 约好的未来的交易价格
• 到期日
• 回报/利润

远期合约的盈亏图

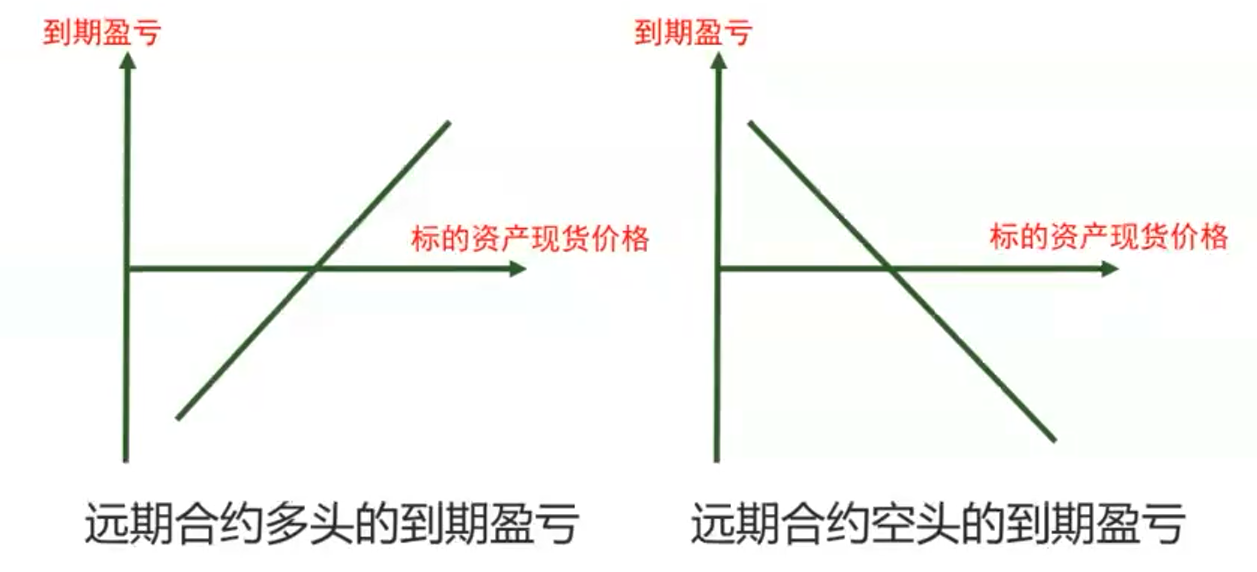
远期合约不保证盈利，但锁定了未来价格，消除了风险

金融远期合约的种类

• 远期利率协议
• 远期外汇协议
• 远期股票合约

远期利率协议

• 买卖双方同意从未来某一商定的时刻开始，在某一特定时期内按协议利率借贷一笔数额确定、以特定货币表示的名利本金的协议

• 远期利率： 1 * 4 3 * 6

远期外汇协议

CNY / CNH / NDF

远期股票合约

• 远期股票合约
  • 在将来某一特定日期特定价格交付一定数量单只股票或一揽子股票的协议

期货与期货市场

金融期货

• 在交易所交易的、协议双方约定在将来某个日期按事先确定的条件（包括交割价格、交割地点和交割方式等）买入或卖出一定标准数量的特定金融工具的标准化协议

金融期货种类

• 股票指数期货
• 利率期货
• 外汇期货

金融期货交易机制

金融期货交易机制的特点

• 交易所内集中交易：信息优势，流动性好
• 标准化合约：流动性好，个性化不足
• 特殊的交易和交割制度：控制信用风险
  • 每日盯市结算（ Marking to Market and Daily Settlement ）
  • 保证金（ Margin ）制度

标准化合约的内容

• 合约规模/交易单位
• 到期时间
• 最小价格波动值
• 每日价格波动限制与交易中止规则（熔断）
• 交割条款
  • 现金交割和实物交割
  • 交割日期和交割地点等
• 头寸限制

远期和期货的比较

• 交易场所不同
• 标准化程度不同
• 违约风险不同
• 合约双方关系不同
• 价格确定方式不同
• 结算方式不同
• 结清方式不同

远期与期货定价

预备知识

投资性资产与消费性资产

• 投资性资产（Investment Assets）

  • 此类资产的持有者以投资为目的

• 消费性资产（Consumption Assets）

  • 持有者以消费为目的

远期价值、远期价格与期货价格

交割价格（ Delivery Price ）

远期价值：远期合约本身的价值

远期价格（ Forward Price ）：

​ ➢ 当下签订远期合约，合约中约定的交割价格

​ ➢ 使得远期价值为零的交割价格

期货价格（ Futures Price ）

远期价格和期货价格的关系

• 当无风险利率恒定且对所有到期日都相同时，其他条件相同的远期价格和期货价格相等

基本假设

主要符号

无收益资产的远期定价

无套利定价法

• 两种资产的未 来现金流相同，则当前的资产价 格也相同。否则，会存在无风险套利的机会。

无收益资产的远期价值

• 无收益资产是指在远期到期前不产生现金流的资产，如贴现债券。
• 构建组合：
  • 组合A ： 一份远期合约多头加上一笔数额为 𝐾𝑒 −𝑟 𝑇−𝑡 的现金（无风险投资）
  • 组合B ： 一单位标的资产

$$
f = S - Ke^{-r(T-t)}
$$

现货-远期平价定理

远期价格：

• F就是使远期合约价值 f 为 零 的交割价格 K
  $$
  F = Se^{r(T-t)}
  $$

无风险资产的现货-远期平价定理： 对于无收益资产而言，远期价格等于其标的资产现货价格的无风险终值

远期价格的期限结构

远期价格的期限结构描述的是不同期限远期价格之间的关系。

• F为T时刻交割的远期价格
• F*为T*时刻交割的远期价格
• r 为 T 时刻到期的无风险利率
• r* 为T*时刻到期的无风险利率

$$
F^{*} = Fe^{r^{*}(T^{*}-t)-r(T-t)}
$$

这就是无红利资产远期价格的期限结构

已知现金收益资产远期定价

已知现金收益的资产

已知现金收益的资产：

• 到期之前会产生完全可预测的现金流的资产

例子：

• 正现金收益的资产：附息债和支付已知现金红利的股票
• 负现金收益的资产：黄金、白银（支付存储成本）

令已知现金收益的现值为I， 对黄金、白银来说，I 为负值

支付已知现金收益资产的远期价值

$$
f = S-I-ke^{-r(T-t)}
$$

支付已知红利资产的远期价格(远期平价公式)

$$
F = (S-I)e^{r(T-t)}
$$

支付已知收益率资产远期合约的定价

远期价值：
$$
f = Se^{-q(T-t)} - Ke^{-r(T-t)}
$$
远期价格：
$$
F = Se^{(r-q)(T-t)}
$$

套利

$$
F = Se^{r(T-t)}
$$

F可以看作S元的本利和，F则是交割价值

• 当F > K 时，套利者可以卖空该标的资产并将所得收入以无风险利率进行投资，期末可获得无风险利率 F - K

• 当F < K 时，套利者可以以无风险利率借入S元，买入标的，并以K元价格卖出远期合约，期末可获得无风险利率K - F

远期和期货的运用

期货完美套期保值

运用远期（期货）进行套期保值

• 投资者在现货市场已有一定头寸和风险暴露
• 运用远期（期货）的相反头寸对冲风险

运用远期（期货）进行套期保值的类型

多头（买入）套期保值

• 运用远期（期货）多头进行套期保值
• 适合担心价格上涨的投资者，锁定未来的买入价格

空头（卖出）套期保值

• 运用远期（期货）空头进行套期保值
• 担心价格下跌的投资者，锁定未来的卖出价格

运用期货或远期进行套期保值，消除了价格风险，但不能保证盈利

不完美套期保值

完美/不完美的套期保值

完美的套期保值

• 完全消除价格风险
• 远期（期货）的到期日、标的资产和交易金额等条件的设定使得远期（期货）需与现货恰好匹配

不完美的套期保值

• 无法完全消除价格风险
• 常态

不完美套期保值的来源：基差风险

基差风险：

• 基差：特定时刻被套期保值的现货价格S 与用以进行套期保值的期货市场价格F之差
  $$
  b = S - F
  $$

• 套期保值到期时基差的不确定性导致了不完美套期保值

基差风险

• 1 单位现货空头 +1 单位期货多头的实际支出
  $$
  S_1 - (F_1-F_0) = F_0 + (S_1-F_1) = F_0 + b_1
  $$

• 1 单位现货多头 +1 单位期货空头的实际收益
  $$
  S_1 + (F_0 - F_1) = (S_1 - F_1) + F_0 = b_1 + F_0
  $$

• F_0总是已知的

• b_1 决定了套期保值是否确定，是否完美套期保值

基差风险的理解

• 基差风险描述了运用远期（期货）进行套期保值时无法完全对冲的价格风险

• 但通过套期保值，投资者将其所承担的风险由现货价格的不确定变化转变为基差的不确定变化，而基差变动的程度总是远远小于现货价格的变动程度，因此不完美套期保值虽然无法完全对冲风险，但还是在很大程度上降低了风险

远期（期货）套期保值策略

期货套期保值的策略

• 合约的选择
• 合约到期日的选择
• 合约头寸方向的选择
  • 多头
  • 空头
• 合约数量的选择

期货合约品种的选择

• 一般原则：选择足够流动性且与被套期保值的现货资产高度相关的合约品种

• 期货合约在大多数情况下流动性较好，且可以采取提前平仓的方式结束头寸，但往往可得的品种较少。另外，期货有特殊的每日盯盘结算与保证金要求

期货合约到期日的选择

• 一般原则：对于实物交割的期货而言，要避免在期货到期的月份中持有期货头寸，以防止逼仓
• 在到期时间无法完全吻合时，通常选择比所需的套期保值月份略晚但尽量接近的期货品种
• 所需套期保值时间较长时，可使用套期保值展期，但可能给套期保值者带来额外的风险

最优套期保值比率的确定

最优套期保值比率
$$
n = \frac{套期保值资产头寸数量}{被套期保值资产头寸数量}
$$

• 最优套期保值比率：能够最大程度地消除被保 值对象价格变动风险

• 存在基差风险时，最优套期保值比率很可能不为 1

股指期货、外汇远期、利率远期、利率期货

股指期货

股指期货概述

股票指数

• 运用统计学中的指数方法编制而成的、反映股市中 总体股价或某类股票价格变动和走势情况的一种相对指标。

股指期货

• 以股票指数作为标的资产的股票指数期货，交易双方约定在将来某一特定时间交收“一定点数的股价指数”的标准化期货合约。

特殊性质：

• 现金结算而非实物交割
• 合约规模非固定
  • 股指期货价格 × 每个指数点所代表的金额

股指期货的定价

一般公式：
$$
F = Se^{(r-q)(T-t)}
$$

外汇远期

FXA 的远期价值与远期汇率
$$
f = Se^{-r_f(T-t)} - Ke^{-r(T-t)}
$$

$$
F = Se^{(r-r_f)(T-t)}
$$

利率平价关系：

• 若𝑟𝑓 > 𝑟, 外汇远期贴水；
• 若𝑟𝑓 < 𝑟 , 外汇远期升水。

远期利率协议

利率远期与期货

• 远期：FRA
• 期货：
  • 存款：欧洲美元期货（短期）
  • 国债：中国5年国债期货（中期）

远期利率协议

远期利率协议（ FRA ）是买卖双方同意从未来 某一商定的时刻开始的一定时期内按协议利率 借贷一笔数额确定、以具体货币表示的名义本金的协议。

互换概述

互换的含义

• 互换（ Swaps ）是两个或两个以上当事人按照商定条件，在约定的时间内交换一系列现金流的合约。
• 互换可以看作是一系列远期的组合
• 互换属于OTC产品，在场外交易

互换的类别

根据现金流计算方式的不同

• 利率互换（ Interest Rate Swap，IRS ）
• 货币互换（ Currency Swap ）
• 其他互换

利率互换

• 在利率互换中，双方同意在未来的一定期限内 根据同种货币的相同名义本金交换现金流，其中一方的现金流根据事先选定的某一浮动利率计算，而另一方的现金流则根据固定利率计算

• 常见期限包括1 年、2 年、3 年、4 年、5 年、 7 年与10 年，也偶见30 年与50 年的利率互换 。

货币互换

• 典型的货币互换是在未来约定期限内将一种货币的本金和固定利息与另一货币的等价本金和固定利息进行交换。

• 利率互换与货币互换之差异：

  • 利率互换：通常无需交换本金，只定期交换利息差额；
  • 货币互换：期初和期末须按照约定的汇率交换不同货币的本金，期间还需定期交换不同货币的利息。

其他互换

基点互换：浮动利率互换

• Constant Maturity Swap (CMS)：LIBOR 与特定期限的 互换利率

• Constant Maturity Treasury Swap (CMT): LIBOR 与特 定期限的美国国债利率

• 我国有七天回购利率（FR007)与3个月Shibor之间的 互换，但很少交易。

互换市场

互换的定价和风险分析

利率互换的定价

互换的定价方法：债券互换，FRA定价

互换风险：

• 信用风险（货币互换风险更大，因为需要交换名利本金）

• 市场风险：

  • 信用风险（货币互换风险更大，因为需交换名利本金）
  • 市场风险：利率风险（利率互换、货币互换）、汇率风险（货币互换 ）

如何对冲市场风险：久期、凸性等分析工具，运用市场上的固定收益产品如欧元美元期货对冲互换中的利率风险； 通过远期外汇协议对冲货币互换的汇率风险。

互换多头：支付固定利率的一方

互换空头：收取固定利率的一方，支付浮动利率

运用债券组合给利率互换定价

$$
B_{fix}为互换合约中分解出来的固定利率债券的价值
$$

$$
B_{fl}为互换合约中分解出来浮动利率债券的价值
$$

$$
多头价值V_{互换} = B_{fl} - B_{fix}
$$

固定利率债券的定价公式：
$$
B_{fix} = \sum_{i=1}^{n}ke^{-r_it_i} + Ae^{-r_nt_n}
$$
浮动利率债券的定价公式：
$$
B_{f1} = (A + k^*)e^{-r_1t_1}
$$

运用远期利率协议给利率互换定价

合理互换利率的确定

合理的互换利率就是使得利率互换价值为零的 固定利率，即
$$
B_{fix} = B_{fl}
$$

互换利率

• 利率互换协议中合理的固定利率就是使得互换 价值为零的利率水平，也就是我们通常所说的 互换利率。

• 现实中的互换利率是市场以一定的计息频率为基础、就特定期限形成的互换中间利率。

货币互换的定价

运用债券组合为货币互换定价

• V_互换: 货币互换的价值
• B_F : 用外币表示的从互换中分解出来的外币债券的 价值
• B_D: 从互换中分解出来的本币债券的价值
• S_0: 即期汇率（直接标价法）

对于收入本币利息、付出外币利息的一方：
$$
V_{互换} = B_D - S_0B_F
$$
对于出本币利息、收入外币利息的一方：
$$
V_{互换} = S_0B_F - B_D
$$

期权和期权市场

期权的定义和种类

期权定义：赋予购买者在规定期限内按双方约定价格购买或出售一定数量某种资产的权力的合约

期权划分：

1. 按权力划分：看涨（买入权力), 看跌
2. 按行政日期划分：美式期权，欧式期权， 百慕大期权

期权与期货的区别：

1. 权利和义务：期权只有买方有权利了
2. 标准化：期货合约标准化； 期权合约不一定
3. 盈利风险
4. 保证金：期货双方需交； 期权多方无需交
5. 套期保值：期权只把不利风险转移，有利风险留给自己

与权证区别：

权证有发行环节，数量有限，影响股本

期权回报与价格分析

期权的回报与盈亏分布

看涨多头（权） : 锁买未买 ：
$$
-C + max(S_T-X, 0)
$$
看涨空头（义）：锁买未卖
$$
C - max(S_T - X, 0)
$$
看跌多头（权）：锁卖未卖
$$
-P + max(X-S_T, 0)
$$

看跌空头（义）：锁卖未买
$$
P - max(X - S_T, 0)
$$
四张图

期权的特性

实值期权：标的价格高于执行价格

平价期权：

虚值期权：

期权价格（价值）= 内在价值（期权回报）+ 时间价值

期权时间价值 = 期权价格 - 期权内在价值

期权时间价值：指期权尚未到期时，标的资产价格波动为期权持有者带来收益的可能性所产生的价值（基于权力义务不对称，多头方获益）

期权时间价值的影响因素：期权剩余有效期越长，标的资产价格发生有利波动概率越大，期权时间价值越大（尤其美式）

平值点：期权内在价值由正值变化到零的标的资产价格的临界点

期权价格的影响因素

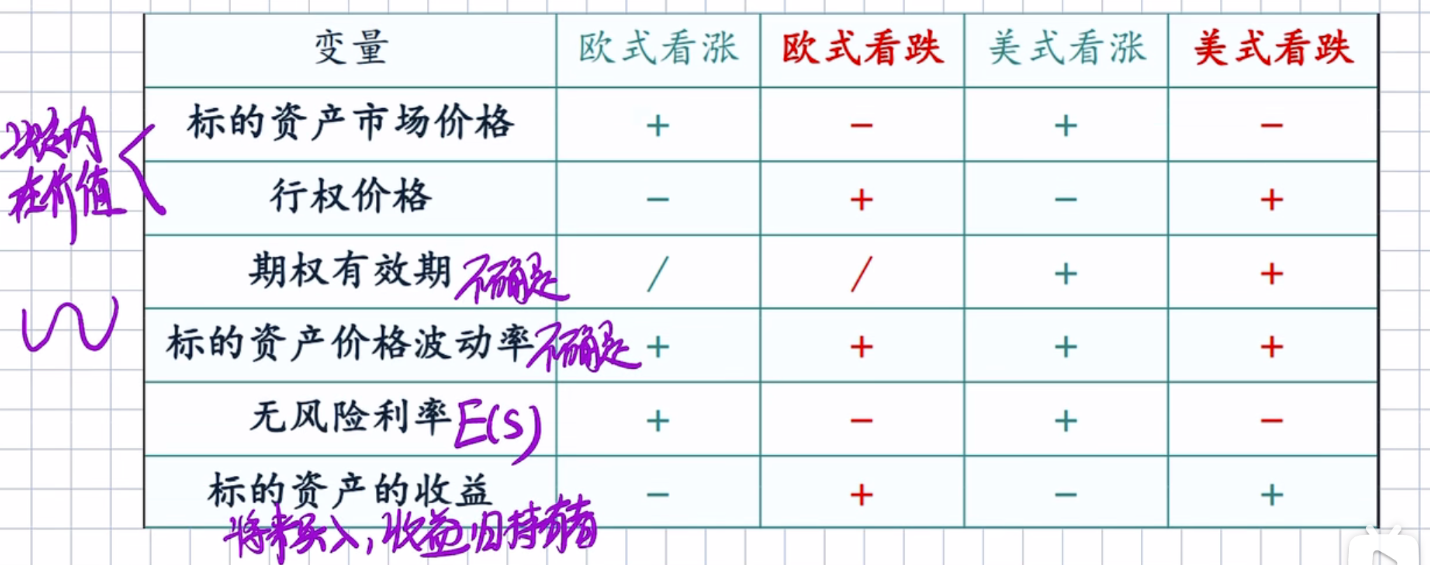
看涨看跌平价定理

看涨看跌期权的平价定理

无收益资产欧式期权：
$$
c + Ke^{-r(T-t)} = p + S
$$
有收益资产的欧式期权：
$$
c + I + Ke^{-r(T-t)} = p + S
$$
无收益美式：
$$
S - X <= C - P <= S - Xe^{-r(T - t)}
$$
有收益美式：
$$
S - I - X <= C - P <= S - Xe^{-r(T-t)}
$$

无收益套利

当 < :买入看涨期，卖空看跌期权和股票，将现金收入 $ -c + p + s $ 进行 n 个月无风险投资，到期可获得 $ (-c+p+s)e^{r*n/12} $, 若到期时股价高于X元，执行看涨期权，若低于X元，则执行看跌期权。无论如何，投资者将都将以X元购买股票，正好用于平仓卖空股票，最终获得收益 $ (-c+p+s)e^{r*n/12} - X $

当 > : 卖出看涨期权，买入看跌期权和股票，需要现金以无风险利率借入， 到期时偿付 $ -(C-P-S)e^{r*n/12} $ ; 若到期时股价低于X, 执行看跌期权，若高于X, 则执行看涨期权。无论如何投资者都将以X卖出股票，最终获得收益 $ X + (C - P - S)e^{r*n/12}$